Siamo abituati a pensare che il punto ha dimensione 0, la retta ha dimensione 1, il piano 2, lo spazio 3 e così via.

Ma l'immagine a lato, che rappresenta la curva di Peano, mostra una retta (dimensione 1) che riempie un quadrato (dimensione 2)

Di conseguenza bisogna cambiare la definizione di dimensione. Kolmogorov (1903-1987) ne propose una derivata dall'idea di misura. Così per la curva di Peano la
                            
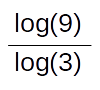
dimensione sarà              cioè 2.

È una retta di dimensione 2!

Ma questa nuova concezione della dimensione può portare anche a risultati non interi. Prendiamo l'esempio della curva di Von Koch.
                                    
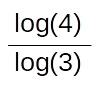
La sua dimensione è               =1,261859...